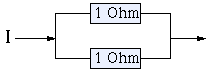
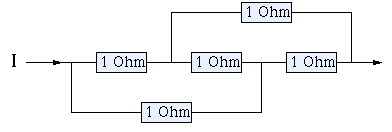
Miss the Mark ★★★

William is playing archery blindfolded. The first arrow he shoots unfortunately misses the bull's-eye. The second arrow misses the bull's-eye even further. William still shoots a third arrow.
The question: How big is the chance that his third shot is also worse than his first shot?
The answer: Click here!