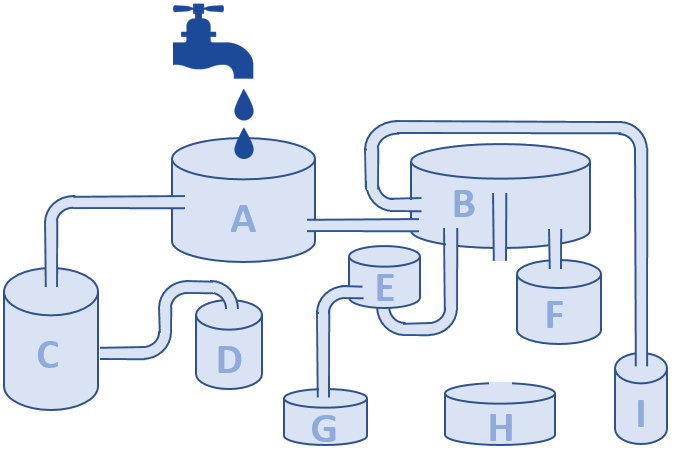
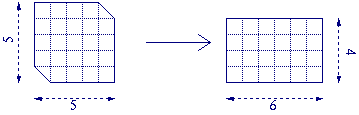
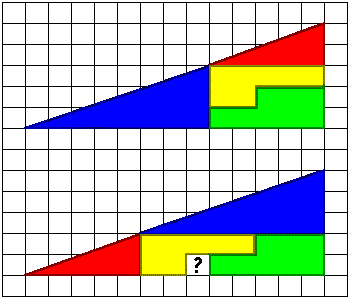
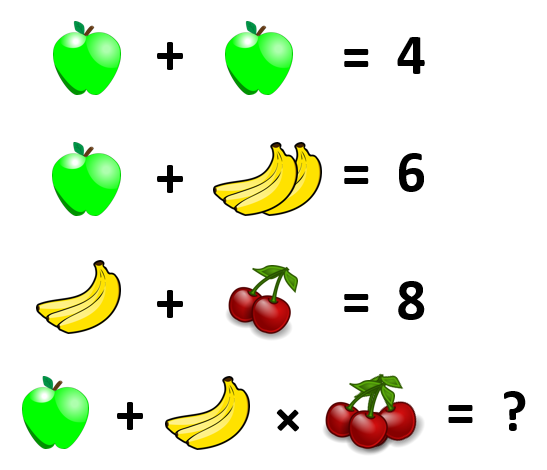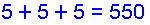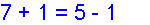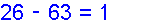Fine Family ★★

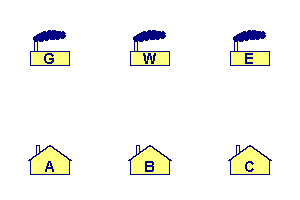
Frank and Susan have six children: Donald, Rebecca, Michael, Faye, Solomon, and Lara. Susan is pregnant of her seventh child, a girl. Frank and Susan have chosen a name for her that fits with the other names.
The question: What will be the name of the seventh child: Jessica, Karen, Abby or Tilly?
The answer: Click here!